Southern California Live Steamers Track Frog Standards

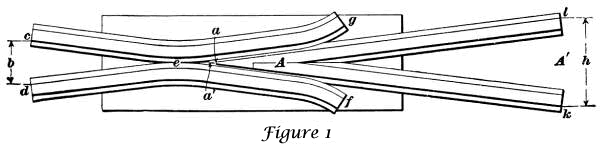
The Frog.—The frog is a device by means of which the rail at the turnout curve crosses the rail of the main track. The frog shown in (FIG 1) is made of rails having the same cross-section as those used in the track, Its parts are as follows: The wedge shaped part A is the tongue, of which the extreme end a is the point. The space b, between the ends c and d of the rails, is the mouth, and the channel which they form at its narrowest point e is the throat. The curved ends f and g are the wings.

That part of the frog between A and A' is called the heel. The width h of the frog is called its spread. Holes are drilled in the ends of the rails c, d, k, and l to receive the bolts used in fastening the rail splices, so that the rails of which the frog is composed form a part of the continuous track.

The Frog Point.—The theoretical point of frog a' (see fig. 1) and the actual point a are quite dissimilar. The reason for making a the point of frog is that if the theoretical and actual point of frog were the same, the point would be so small that the first blow inflicted by a passing locomotive or car would completely destroy it. The frog point is accordingly placed at a, where its width is about ¼ of an inch.

The Frog Number.—The number of a frog is the ratio of its length to its breadth, i.e., the quotient of its length divided by its breadth.

Thus, in fig. 1, if the length a' 1, from point to heel of frog is 5 feet, or 60 inches, and the breadth h of the heel is 15 inches, the number of the frog is the quotient of 60 ÷ 15 = 4. Theoretically, the length of the frog is the distance from a to the middle point of a line drawn from k to 1; practically, we take as the length the distance from a to 1. As it is often difficult to determine the exact point a of the frog, a more accurate method of determining the frog number is to measure the entire length dl of the frog from mouth to heel, and divide this length by the sum of the mouth width b and the heel width h. The quotient will be the exact number of the frog.

For example, if in fig 1, the total length d l of the frog is 7 feet 4 inches, or 88 inches, and the width h is 15 inches, and the width b of the mouth is 7 inches, then the frog number is 88 ÷ (15 + 7) = 4. Frogs are known by their numbers. That in fig 1 is a No. 4 frog.

The Frog Angle.—The frog angle is the angle formed by the gauge lines of the rails, which form its tongue. Thus, in fig 1, the frog angle is the angle l a' k. The amount of the angle may be found as follows: The tongue and heel of the frog form an isosceles triangle (see fig. 2). By drawing a line from the point a of the frog to the middle point b of the heel c d, we form a right-angled triangle, right-angled at b.

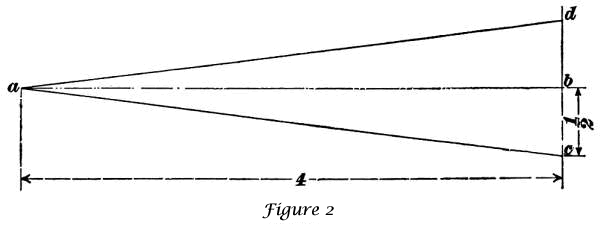
The perpendicular line a b, bisects the angle a, and, by rule 5, Art. 754, we have tan ½ a = b c/a b. The dimensions of the frog point given in fig. 2 are not the same as those given in fig 1, but their relative proportions are the same, viz., the length is four times the breadth. The length a b = 4, and the width c d = 1; hence, b c= ½. Substituting these values, we have tan ½ a = ½/4 = one-eighth = 0.125. Whence, ½ a = 7º 7½', and a = 14º 15'; that is, the angle of a No. 4 frog is 14º 15'.

Normal frog numbers run from 4 to 12, including half numbers, the spread of the frog increasing as the number decreases. Below is a list of curve radii based on frogs from 4 to a hypothetical 16 in .5 increments.

Source material Catskill Archives, radii by FLTenWheeler